Generating random vectors from a Gaussian copula
If we have a Gaussian copula \(C_R(\mathbf{u})\), we can generate random vectors
from it using the following
procedure:
- Perform Cholesky decomposition of the correlation matrix \(R=AA^T\) where
\(A\) is the lower triangular matrix - Generate a \(d\)-dimensional iid standard normal vector \(\mathbf{z}\)
- Multivariate normal random vector to generate is then
\(\mathbf{x} = A\mathbf{z}\), with the corresponding copula vector
\(\mathbf{u} = (\Phi(x_1), \cdots, \Phi(x_d))\)
This is exactly the same procedure to generate multivariate Gaussian random
variables from the covariance matrix \(\Sigma\), only this time we use
correlation matrix \(R\) instead. That makes sense because \(\Sigma\) and
\(R\) are related:
that is, diagonal of \(R\) is always 1 and off-diagonal terms are
\(\frac{E}{\sigma(X_i)\sigma(X_j)}=\frac{\sigma_{ij}}{\sigma_i\sigma_j}\)
Up to here, we can see that the copula lost the information of mean and
variance of individual components \(X_i\) of \(\mathbf{X}\), as it focus only
on their correlation. The random vector generated from the copula is not the
same as the original distribution, but scaled and shifted. This can be seen
from the following plot:
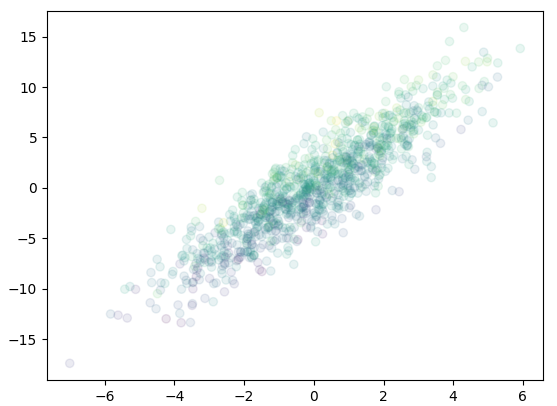
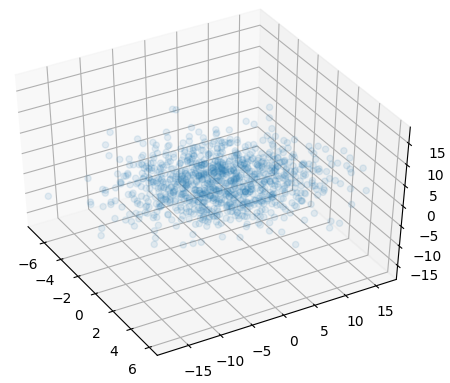
or equiv 3D scatter plot:
and the following is the same plot using Gaussian copula function (i.e. using
the correlation matrix):
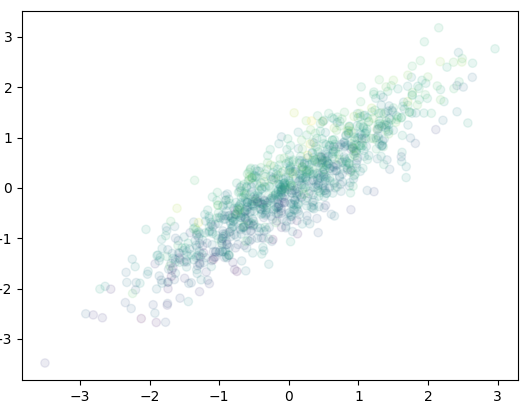
and the 3D version:
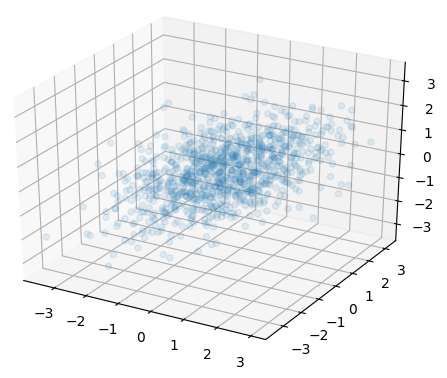
So we see, using the correlation matrix to generate the random vectors is like
transforming the version of using covariance matrix to standard normal, as we
lost the information of relative scale of variance in each dimension. Because of
this, we do not make it any easier to generate multivariate random variables
using copula function.
Vine Copulas¶
In addition, Copulas also implements Vine Copulas. The Vine copulas work by building a vine (a set of trees) over the different columns in the dataset and estimating the pairwise (i.e. bivariate) relationship between the nodes on every edge.
There are three types of Vine copulas: direct, regular, and center.
:
from copulas.multivariate import VineCopula
center = VineCopula('center')
regular = VineCopula('regular')
direct = VineCopula('direct')
center.fit(data)
regular.fit(data)
direct.fit(data)
center_samples = center.sample(1000)
regular_samples = regular.sample(1000)
direct_samples = direct.sample(1000)
:
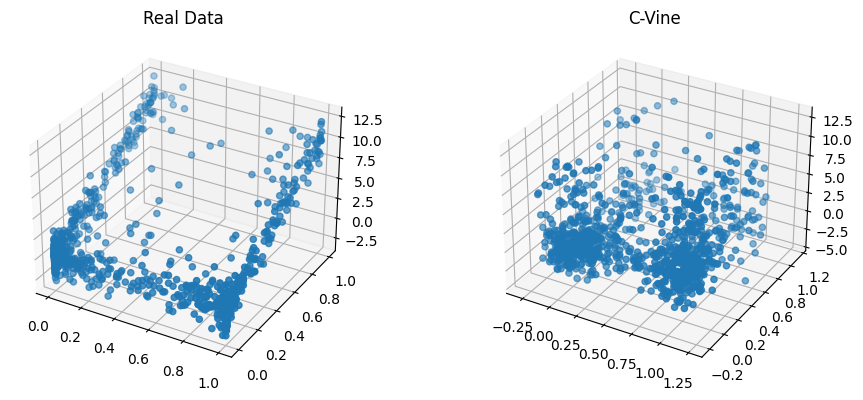
from copulas.visualization import side_by_side
side_by_side(scatter_3d, {'Real Data' data, 'C-Vine' center_samples})
side_by_side(scatter_3d, {'R-Vine' regular_samples, 'D-Vine' direct_samples})

Неподвижные звёзды и созвездия в магии
Маги во все времена использовали знания астрологии, при изготовлении талисманов для достижения желаемых результатов церемонии должны были просходить при наиболее подходящих планетарных конфигурациях. В большинстве дошедших до нашего времени гримуаров по астрологической магии речь идёт о создании талисманов, причем этот процесс связан с семью планетами, известными древним. Однако адепты средневековья и даже поздней античности не пренебрегали неподвижными звёздами и созвездиями. Хотя применялись они нечасто, до нас дошли записи о посвященных им талисманах и амулетах.
Так, в греческих магических папирусах (PGM) присутствуют ритуалы призыва силы созвездия Большой Медведицы и создания амулета, связанного с этим созвездием. В одном из папирусов (PGM IV) приводится ритуал, призывающий созвездие Медведицы и её силы и называется «Медвежья чара для достижения любых целей«. В этом тексте сила созвездия Медведицы призывается и заклинается именами греческих богов, в частности, именами Гелиоса:
В другом тексте папирусов приводится способ создания амулета созвездия Большой Медведицы «для свершения чего угодно».
В средневековых гримуарах приводятся способы изготовления талисманов звёзд, метод обычно заключался в том, что на металле или камне, которым управляет определенная звезда, гравировали соответствующий этой звезде символ или образ. Кроме металлов и камней, иногда использовался девственный пергамент. Все работы выполнялись при подходящих астрологических условиях, обычно предлагалось выбирать время, когда звезда восходит, находится в соединении с Луной, Солнцем или занимает выделенное положение в доме. Изготоваленный талисман окуривался благовониями, созданными из специально подобранных трав, потом его носили на шее в мешочке из шелка или на пальце, если талисман был изготовлен в форме кольца с соответствующим камнем.
Списки соответствий камней, печати, образы звезд и способы изготовления талисманов приведены, в частности, в манускрипте Гермеса «О 15 неподвижных звёздах» из оксфордской библиотеки (Bodleian MS. 52) и в книге Агриппы «Оккультная Философия». Например, у Агриппы звезде Алголь соответствуют камень алмаз, трава полынь и черный морозник, а в качестве образа отрубленная человеческая голова и утверждается, что подобный талисман «помогает добиться прошений; даёт неустрашимость и великодушие, охраняет тело, оберегает от злых чар, обращает колдовство и злые чары на тех, кто их наслал».
Common parametric copula families
We now give a more general definition of bivariate copulas.
The copulas we have introduced so far are all derived from bivariate distributions. In other words, it goes from the joint distribution \(F\) on the left-hand side of the following equation to the copula \(C\) and marginals \(F_j\) on the right-hand side.
$$F(x_1, x_2) = C(F_1(x_1), F_2(x_2)).$$
Given the general definition of the copula, some copula families \(C\) can further be defined explicitly.
This allows us to go from the right-hand side to the left-hand side; that is, linking two marginals using a copula to get a joint distribution.
Below are shown some commonly used parametric bivariate copula families, where \(\rho, \nu\) and \(\delta\) are the parameters.
| Copula family | Copula CDF |
|---|---|
| Gaussian | \(\Phi_2 \left( \Phi^{-1}(u_1), \Phi^{-1}(u_2); \rho \right)\) |
| t | \( T_{2, \nu} \left(T_{1, \nu}^{-1}(u_1), T_{1, \nu}^{-1}(u_2); \rho \right) \) |
| Frank | \( -\delta^{-1} \log \left( \frac{1 — e^{-\delta} — (1 — e^{-\delta u_1}) (1 — e^{-\delta u_2})} {1-e^{-\delta}} \right) \) |
| MTCJ | \( (u_1^{-\delta} + u_2^{-\delta} — 1)^{-1/\delta} \) |
| Joe | \( 1 — \left( (1-u_1)^{\delta} + (1-u_2)^{\delta} — (1-u_1)^{\delta} (1-u_2)^{\delta} \right)^{1/\delta} \) |
| Gumbel | \( \exp \left( -\left( (-\log u_1)^{\delta} + (-\log u_2)^{\delta} \right)^{1/\delta} \right) \) |
Figure 1 shows the constructed bivariate joint distributions using the copula families above and univariate standard normal distributions (i.e., \(F_1 = F_2 = \Phi\)).
Reflected copula
Given \( (U_1, U_2) \sim C \), the reflected copula \(\widehat{C}\) is defined as the copula of \( (1-U_1, 1-U_2) \). That is,
\begin{align}
\widehat{C}(u_1, u_2) &=
\mathbb{P}(1 — U_1 \leq u_1, 1 — U_2 \leq u_2)
\newline
&=
\mathbb{P}(U_1 \geq 1 — u_1, U_2 \geq 1 — u_2).
\end{align}
The reflected copula \(\widehat{C}\) is handy when studying the upper and lower tail properties of a copula, as we will see later.
To facilitate the analysis, we calculate the following probability (survival function):
\begin{align}
\mathbb{P}(U_1 > v_1, U_2 > v_2)
&=
1 — \mathbb{P}(U_1 \leq v_1 \mbox{ or } U_2 \leq v_2)
\newline
&=
1 — \mathbb{P}(U_1 \leq v_1) — \mathbb{P}(U_2 \leq v_2) + \mathbb{P}(U_1 \leq v_1, U_2 \leq v_2)
\newline
&=
1 — v_1 — v_2 + C(v_1, v_2).
\end{align}
The second equality is due to the inclusion–exclusion principle.
Finally, we have
$$\widehat{C}(u_1, u_2) = u_1 + u_2 — 1 + C(1-u_1, 1-u_2).$$
Transforming random variables
Let’s start by sampling uniformly distributed values between 0 and 1:
Next, we want to transform these samples so that instead of uniform they are now normally distributed. The transform that does this is the inverse of the cumulative density function (CDF) of the normal distribution (which we can get in with ):
If we plot both of them together we can get an intuition for what the inverse CDF looks like and how it works:
As you can see, the inverse CDF stretches the outer regions of the uniform to yield a normal.
We can do this for arbitrary (univariate) probability distributions, like the Beta:
Or a Gumbel:
In order to do the opposite transformation from an arbitrary distribution to the uniform(0, 1) we just apply the inverse of the inverse CDF – the CDF:
Rank correlations
Correlation coefficients are useful in summarizing the dependence structure between two variables using a single number.
Pearson’s correlation is probably the most commonly used one.
However, it is known that Pearson’s correlation between \(X\) and \(X^2\) is zero for \(X \sim \mathcal{N} (0, 1)\).
This is often used as an example to illustrate that Pearson’s correlation only measures linear correlation; it is not invariant under increasing transformations.
In nonparametric statistics, rank correlations, such as Spearman’s rho and Kendall’s tau, are defined by the ranks of the data rather than the data itself.
As a result, they are invariant under increasing transformations.
Since copulas are also independent of marginals, there should be a natural connection between copulas and rank correlations.
In fact, both Spearman’s rho and Kendall’s tau can be defined directly as functionals of a copula.
-
Spearman’s rho:
$$
\rho_S( C ) = \iint_{^2}
uv \, \mathrm{d} C(u, v)
-3.
$$ -
Kendall’s tau:
$$
\rho_\tau( C ) = \iint_{^2}
C(u, v) \, \mathrm{d} C(u, v).
$$
The integrals are Riemann–Stieltjes integrals.
The parameters of bivariate copulas in Figure 1 are chosen such that their Kendall’s tau all equals 0.5.
Примеры использования копулы
Копула может быть использована в разных областях, где необходимо описать зависимости между переменными. Рассмотрим несколько примеров:
- Финансы: копула используется для моделирования рисков инвестиционного портфеля. Например, можно определить вероятность того, что акции двух компаний будут расти вместе или падать вместе.
- Страхование: копула позволяет оценить вероятность наступления нескольких событий одновременно. Например, вероятность того, что наступят различные страховые случаи у нескольких клиентов компании.
- Экология: копула может быть использована для анализа зависимости различных факторов, влияющих на экологическую ситуацию в регионе. Например, зависимость уровня загрязнения воздуха от количества транспорта и погодных условий.
Также копула может быть использована в других областях, требующих моделирования зависимостей между переменными, например, в метеорологии, маркетинге, медицине и т.д.
Самые значимые неподвижные звезды
Решение, какие звёзды использовать каждый астролог принимает сам. Первая задача в работе с неподвижными звёздами заключается в том, чтобы найти наиболее важные взаимодействия самых важных звёзд. Некоторые звёзды захватывали воображение многих народов своей яркостью или расположением в ключевых точках солнечного года. Ниже приведена таблица самых важных звёзд, влияние которых учитывать совершенно необходимо:
| Звезда | Созвездие | Природа | Влияние |
|---|---|---|---|
| Четыре королевские звезды Персии: древние кардинальные точки | |||
| Альдебаран | Телец | Марс | Почёт, ум, красноречие, стойкость, цельность натуры, популярность, храбрость, свирепость, бунтарство. Предвещает славу, признание, власть и богатство. |
| Антарес | Сердце Скорпиона | Марс и Юпитер | Воинственный и злотворный характер. Злоба, разрушение, свободолюбие, вольнодумство, зловещие предзнаменования. Почести и богатство. |
| Фомальгаут | Южная Рыба | Венера и Меркурий | Счастливая и мощная звезда, переход от материального к духовному, почести, бессмертие имени. |
| Регул | Сердце Льва | Марс и Юпитер | Сила духа, возвышенные идеалы, щедрость, великодушие, смелость, амбициозность, властолюбие, лидерские качества, тюрьма, насильственная смерть. |
| Звёзды Ориона | |||
| Ригель | Ступня Ориона | Юпитер и Сатурн | Почет, слава, богатство, признание, изобретательские способности, благожелательность, способности в области механики. |
| Бетельгейзе | Правое плечо Ориона | Марс и Меркурий | Лидерство, изобретательность, военная слава, успех и продвижение в карьере, богатство |
| Беллатрикс | Левое плечо Ориона | Марс и Меркурий | Высокие почести, но и риск их неожиданной потери, слава, богатство, видные друзья, несчастные случаи |
| Ниболее трудные и вредоносные звёзды | |||
| Алголь | Персей, голова Медузы Горгоны | Сатурн и Юпитер | Беды, насилие, отрубание головы, повешение, насильственная смерть, тяжелая болезнь |
| Менкар | Кит | Сатурн | Болезни, бесчестие, разорение, травмы от диких животных, неудачи, наследство |
| Фациес | Стрелец | Солнце и Марс | Плохое зрение, несчастные случаи, насильственная смерть |
| Капулус | Меч Персея | Марс и Меркурий | Вызывает слепоту или плохое зрение |
| Зосма | Спина Льва | Сатурн и Венера | Эгоизм, себялюбие, аморальность, доход от неправедных дел, злоба, меланхолия, бесстыдство, неразумность, опасность отравления. |
| Другие основные звёзды | |||
| Сириус | Большой Пёс | Юпитер и Марс | Честь, слава, богатство, пламенность, самоотверженность, преданность, страсть, высокое положение, хорошая репутация, прибыль. |
| Спика | Дева | Венера и Марс | Успех, слава, богатство, хороший характер, любовь к искусству, науке, почет, благоприятно для священнослужителей и юристов. |
| Канопус | часть руля корабля Арго | Сатурн и Юпитер | Набожность, консерватизм, широкий кругозор, глубокие знания, дальние путешествия, образовательная деятельность, известность, высокое положение, богатство. |
Student Copula¶
An alias of the is . We can use either as they both refer to the same underlying structure.
:
from copulae import StudentCopula degrees_of_freedom = 5.5 # some random number, unnecessary to specify df but done for demonstration purposes t_cop = StudentCopula(dim=ndim, df=degrees_of_freedom) t_cop.fit(residuals)
:
<copulae.elliptical.student.StudentCopula at 0x20934674250>
The Student Copula differs from the Gaussian Copula in that it has one additonal parameter, the degrees of freedom . This can be seen from the summary.
:
t_cop.summary()
:
Parameters
Degree of Freedom10.544336897837123Correlation Matrix
| 1.000000 | 0.177448 | -0.374353 | 0.092292 | 0.111153 | 0.071979 | 0.265017 |
| 0.177448 | 1.000000 | 0.525289 | -0.055004 | -0.077388 | -0.065854 | 0.181237 |
| -0.374353 | 0.525289 | 1.000000 | 0.057958 | 0.013242 | 0.060967 | 0.018374 |
| 0.092292 | -0.055004 | 0.057958 | 1.000000 | 0.630141 | 0.939847 | 0.579627 |
| 0.111153 | -0.077388 | 0.013242 | 0.630141 | 1.000000 | 0.716690 | 0.411565 |
| 0.071979 | -0.065854 | 0.060967 | 0.939847 | 0.716690 | 1.000000 | 0.558953 |
| 0.265017 | 0.181237 | 0.018374 | 0.579627 | 0.411565 | 0.558953 | 1.000000 |
Fit Summary
| Fit Summary | |
|---|---|
| Log Likelihood | -838.7958878695256 |
| Variance Estimate | Not Implemented Yet |
| Method | Maximum pseudo-likelihood |
| Data Points | 394 |
| Optimization Setup | Results | ||
|---|---|---|---|
| bounds | x | ||
| options | {‘maxiter’: 20000, ‘ftol’: 1e-06, ‘iprint’: 1, ‘disp’: False, ‘eps’: 1.5e-08} | fun | -838.7958878695256 |
| method | SLSQP | jac | |
| None | None | nit | 31 |
| None | None | nfev | 771 |
| None | None | njev | 31 |
| None | None | status | |
| None | None | message | Optimization terminated successfully |
| None | None | success | True |
:
t_cop.params
:
StudentParams(df=10.544336897837123, rho=array())
Двумерная копула[]
Двумерная копула — это функция CI2→I{\displaystyle C:I^{2}\rightarrow I} такая что:
1) C(,x)=C(x,)={\displaystyle C(0,x)=C(x,0)=0} для всех x∈I{\displaystyle x\in I};
2) для a,b,c,d∈I{\displaystyle a,b,c,d\in I}, где a≤b{\displaystyle a\leq b} и c≤d{\displaystyle c\leq d}:
VC(a,b×c,d)=C(b,d)−C(a,d)−C(b,c)+C(a,c)≥{\displaystyle V_{C}(\times )=C(b,d)-C(a,d)-C(b,c)+C(a,c)\geq 0}.
Функцию VC{\displaystyle V_{C}} в свойстве 2 называют C{\displaystyle C}-объемом прямоугольника a,b×c,d{\displaystyle \times }.
N{\displaystyle N}-мерная копула — это многомерная совокупная функция распределения с равномерно распределенными на ,1{\displaystyle } маргиналами.
Свойства копулы и их важность
Свойства копулы:
- Симметрия: копула должна быть симметричной относительно диагонали. Это означает, что вероятность совместного наступления двух событий не должна зависеть от порядка, в котором они рассматриваются. Например, вероятность того, что тело будет двигаться вверх и вправо, должна быть такой же, как и вероятность движения вниз и влево.
- Положительная однородность: копула должна быть положительно однородной. Это означает, что любое увеличение вероятности одного события должно приводить к увеличению вероятности всех других событий. Например, если вероятность того, что человек заболеет, увеличивается, то вероятность того, что он также заплатит за лекарства, должна также увеличиваться.
- Монотонность: копула должна быть монотонной. Это означает, что если одно событие имеет большую вероятность, чем другое, то вероятность их совместного наступления должна быть не меньше вероятности более вероятного события. Например, если вероятность того, что счастливый билетик окажется у женщины, выше, чем вероятность, что он окажется у мужчины, то вероятность того, что он окажется у женщины-мужчины, должна быть не меньше, чем у просто женщины или просто мужчины.
Значимость свойств копулы:
Свойства копулы являются ключевыми при определении совместных распределений. Правильный выбор копулы зависит от свойств и особенностей исследуемых данных. Например, если данные связаны с логнормальным распределением, то следует использовать копулу с инвариантом логнормального распределения. Также свойства копулы важны при анализе и предсказании рисков в различных областях, таких как финансы, страхование, маркетинг и т.д.
Introduction
Copula is a great statistical tool to study the relation among multiple random variables: By focusing on the joint cumulative density of quantiles of marginals, we can bypass the idiosyncratic features of marginal distributions and directly look at how they are “related”.
Indeed, traders and analysts have been using copula to exploit statistical arbitrage under the pairs trading framework for some time, and we have implemented some of the most popular methods in ArbitrageLab. However, it is natural to expand beyond dealing with just a pair of stocks: There already exist a great amount of competing stat arb methods alongside copula, thinning the potential alpha. It is also intuitive for humans to think about relative pricing among 2 stocks, whereas for higher dimensions it is not so easy, and left great opportunities for quantitative approaches.
Copula itself is not limited to just 2 dimensions. You can expand it to arbitrarily large dimensions as you wish. The disadvantage comes from the practicality side: originally when probabilists created copula, in order to do further analysis theoretically they focus on a very small subset of copulas that have strict structural assumptions about their mathematical form. In reality, when there are only 2 dimensions, under most cases you can still model a pair of random variables reasonably well with the existing bivariate copulas. However when it goes to higher dimensions, the copula model becomes quite rigid and tends to lose a lot of useful details.
Therefore, vine copula is invented exactly to address this high dimensional probabilistic modeling problem. Instead of using an N-dimensional copula directly, it decomposes the probability density into conditional probabilities, and further decomposes conditional probabilities into bivariate copulas. To sum up:
The idea is that we decompose the high dimensional pdf into bivariate copulas (densities) and marginal densities.
Примеры применения копулы в статистике
Моделирование многомерных распределений: Копула часто используется для моделирования совместных распределений нескольких случайных величин. Она позволяет описать зависимость между ними, что невозможно сделать другими методами.
Статистический анализ рисков: Копула применяется в анализе рисков, когда необходимо оценить вероятность наступления события при определенных условиях. Например, использование копулы помогает оценить вероятность того, что две акции упадут одновременно.
Оценка зависимости между переменными: Копула также может быть полезна при оценке зависимости между двумя переменными. Она используется в эконометрике, финансовых исследованиях и других областях, где необходимо оценить силу связи между переменными.
Оценка вероятности кредитного дефолта: Копула применяется в банковской практике при оценке вероятности кредитного дефолта нескольких заемщиков. Она позволяет учесть зависимости между заемщиками, что улучшает точность оценки рисков.
Моделирование экстремальных событий: Копула может использоваться для моделирования экстремальных событий, например, наводнений или землетрясений. Она позволяет описать вероятность наступления нескольких событий одновременно.






















