Понятие отрицательного числа
Отрицательное число – это число, которое меньше нуля. В алгебре отрицательные числа обозначаются с помощью минуса перед числом. Например, -3, -5, -10 – это отрицательные числа.
Квадрат отрицательного числа – это результат умножения числа на само себя. Вычислить квадрат отрицательного числа можно следующим образом: сначала возьмите модуль числа (отбросит знак), а затем возведите его в квадрат. Например, чтобы найти квадрат числа -4, мы должны взять модуль -4, то есть просто число 4, и возвести его в квадрат: 4 * 4 = 16. Таким образом, квадрат отрицательного числа -4 равен 16.
Важно отметить, что квадрат любого числа всегда положительный результат. Это связано с тем, что умножение чисел всегда дает положительное значение, даже если один из множителей отрицательный
Квадрат отрицательного числа также будет положительным числом, независимо от исходного числа.
Выводит информацию о квадрате отрицательного числа можно в виде таблицы, где в первый столбец собраны отрицательные числа, а во втором столбце представлены результаты возведения этих чисел в квадрат. Такая таблица помогает наглядно представить, как возведение отрицательных чисел в квадрат приводит к положительным результатам.
| Отрицательное число | Квадрат отрицательного числа |
|---|---|
| -1 | 1 |
| -2 | 4 |
| -3 | 9 |
| -4 | 16 |
| -5 | 25 |
Что такое отрицательное число?
Отрицательное число — это число, которое меньше нуля. В отличие от положительных чисел, отрицательные числа обозначаются со знаком минус («-«). Квадрат отрицательного числа будет всегда положительным числом.
Для наглядного примера, рассмотрим число -5. Если возведем его в квадрат, получим результат 25. Таким образом, квадрат отрицательного числа будет равен положительному числу.
Отрицательные числа широко применяются в математике, физике, экономике и других науках. Они используются для обозначения задолженностей, потерь, отрицательных изменений и других ситуаций, когда величина уменьшается или направление движения обратно.
При работе с отрицательными числами важно учитывать правила математических операций. Например, при умножении двух отрицательных чисел получаем положительное число, а при делении отрицательного числа на положительное — отрицательное число
В заключение, отрицательные числа представляют собой важный элемент в математике и других науках. Их применение позволяет точнее описывать различные явления и процессы, где величины могут быть меньше нуля и направлены в обратную сторону.
Как определить отрицательное число?
Определить, является ли число отрицательным, можно с помощью нескольких способов. Один из самых простых способов — это проверить знак числа. Если число меньше нуля, то оно является отрицательным.
Еще один способ — это взять число и возвести его в квадрат. Если полученный результат положительный, то исходное число было отрицательным. Если же результат отрицательный, то исходное число было положительным.
Если число записано в виде десятичной дроби, то определение его знака может быть немного сложнее
В этом случае можно обратить внимание на знак перед запятой. Если перед запятой стоит знак «-«, то число является отрицательным
Также есть математические методы определения знака числа, например, использование функции знака. Функция знака возвращает -1 для отрицательных чисел, 0 для нуля и 1 для положительных чисел.
Понятие равносильных уравнений
Равносильными называются такие уравнения, имеющие одни и те же корни, или же те, в которых корней нет.
Определения такого типа часто встречаются в различных учебниках. Приведем несколько примеров.
Уравнение f ( x ) = g ( x ) считается равносильным уравнению r ( x ) = s ( x ) , если у них одинаковые корни или у них обоих нет корней.
Уравнения с одинаковыми корнями считаются равносильными. Также ими считаются два уравнения, одинаково не имеющие корней.
Если уравнение f ( x ) = g ( x ) имеет то же множество корней, что и уравнение p ( x ) = h ( x ) , то они считаются равносильными по отношению друг к другу.
Когда мы говорим о совпадающем множестве корней, то имеем в виду, что если определенное число будет корнем одного уравнения, то оно подойдет в качестве решения и другому уравнению. Ни одно из уравнений, являющихся равносильными, не может иметь такого корня, который не подходит для другого.
Приведем несколько примеров таких уравнений.
Например, равносильными будут 4 · x = 8 , 2 · x = 4 и x = 2 , поскольку каждое из них имеет только один корень – двойку. Также равносильными будут x · 0 = 0 и 2 + x = x + 2 , поскольку их корнями могут быть любые числа, то есть множества их решений совпадают. Также равносильными будут уравнения x = x + 5 и x 4 = − 1 , каждое из которых не имеет ни одного решения.
Для наглядности рассмотрим несколько примеров неравносильных уравнений.
К примеру, таковыми будут x = 2 и x 2 = 4 , поскольку их корни отличаются. То же относится и к уравнениям x x = 1 и x 2 + 5 x 2 + 5 , потому что во втором решением может быть любое число, а во втором корнем не может быть 0 .
Определения, данные выше, подойдут и для уравнений с несколькими переменными, однако в том случае, когда мы говорим о двух, трех и более корнях, более уместно выражение «решение уравнения». Таким образом, подытожим: равносильные уравнения – это те уравнения, у которых одни и те же решения или их совсем нет.
Возьмем примеры уравнений, которые содержат несколько переменных и являются равносильными друг другу. Так, x 2 + y 2 + z 2 = 0 и 5 · x 2 + x 2 · y 4 · z 8 = 0 включают в себя по три переменных и имеют только одно решение, равное 0 , во всех трех случаях. А пара уравнений x + y = 5 и x · y = 1 равносильной по отношению друг к другу не будет, поскольку, например, значения 5 и 3 подойдут для первого, но не будут решением второго: при подстановке их в первое уравнение мы получим верное равенство, а во второе – неверное.
Решение неполных квадратных уравнений
Как мы уже знаем, есть три вида неполных квадратных уравнений:
- ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
- ax 2 + c = 0, при b = 0;
- ax 2 + bx = 0, при c = 0.
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.
Как решить уравнение ax 2 = 0
Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.
Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.
Пример 1. Решить −6x 2 = 0.
- Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
- По шагам решение выглядит так:
Как решить уравнение ax 2 + с = 0
Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
- перенесем c в правую часть: ax 2 = — c,
- разделим обе части на a: x 2 = — c/а.
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.
| В двух словах |
|---|
Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:
не имеет корней при — c/а 0.
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
- Перенесем свободный член в правую часть:
Разделим обе части на 8:
В правой части осталось число со знаком минус, значит у данного уравнения нет корней.
Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.
Как решить уравнение ax 2 + bx = 0
Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:
Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:
Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0
Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
Решить линейное уравнение:
0,5x = 0,125, х = 0,125/0,5
Значит корни исходного уравнения — 0 и 0,25.
Ответ: х = 0 и х = 0,25.
Как разложить квадратное уравнение
С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:
Формула разложения квадратного трехчлена
Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2).
Сравнение корней
Зачем нам учиться сравнивать числа, содержащие квадратный корень?
Очень просто. Часто, в больших и длиииинных выражениях, встречающихся на экзамене, мы получаем иррациональный ответ (помнишь, что это такое? Мы с тобой сегодня об этом уже говорили!)
Полученные ответы нам необходимо расположить на координатной прямой, например, чтобы определить, какой интервал подходит для решения уравнения. И вот здесь возникает загвоздка: калькулятора на экзамене нет, а без него как представить какое число больше, а какое меньше? То-то и оно!
Например, определи, что больше: \( \displaystyle 3\sqrt{7}\) или \( \displaystyle 2\sqrt{17}\)?
Сходу и не скажешь. Ну что, воспользуемся разобранным свойством внесения числа под знак корня?
Тогда вперед:
Ну и, очевидно, что чем больше число под знаком корня, тем больше сам корень!
Т.е. если \( \displaystyle 68>63\), значит, \( \displaystyle \sqrt{68}>\sqrt{63}\).
Отсюда твердо делаем вывод, что \( \displaystyle 3\sqrt{7}<2\sqrt{17}\).
Таблица квадратов натуральных чисел 100 до 200
|
1012 = 10 201 |
1112 = 12 321 |
1212 = 14 641 |
1312 = 17 161 |
1412 = 19 881 |
|
1512 = 22 801 |
1612 = 25 921 |
1712 = 29 241 |
1812 = 32 761 |
1912 = 36 481 |
Нахождение степеней с иррациональным показателем
Иногда возникает необходимость нахождения значения степени, показатель которой представляет собой иррациональное число. Проблема заключается в том, что найти точное значение подобного выражения невозможно. Однако для решения любой практической задачи, как правило, достаточно нахождения значения степенного выражения с определенной степенью точности. В этом случае иррациональный показатель округляется до требуемого десятичного знака, после чего вычисление осуществляется согласно правилам, принятым для дробного показателя.
Рассмотрим решение подобной задачи на конкретном примере:
Пример 13
Предположим, что нам необходимо найти значение выражения 2 в степени √2. Показатель степени является иррациональным числом. В виде бесконечной десятичной дроби оно может быть записано следующим образом:
√2 = 1,41421356…
Найдем значение выражения с различной степенью приближения.
Вариант 1.
Округлим значение иррационального числа до двух цифр после запятой и найдем приближенное значение степени:
\
\
Вариант 2.
Округлим значение иррационального числа до четырех цифр после запятой и найдем приближенное значение степени:
\
\
Можно видеть, что полученные значения различаются во втором знаке после запятой, при этом второе значение является более точным.
В большинстве случаев вычисление степеней с иррациональными показателями является сложной задачей, для решения которой используется вычислительная техника.
Тригонометрическая и показательная форма комплексных чисел
Попробуем на примере конкретного комплексного числа z=1-i записать его в тригонометрической форме. Для этого разберем части этого числа:
- —действительная часть;
- мнимая часть.
Далее потребуется определить модуль и аргумент комплексного числа:
Таким образом, тригонометрическая форма комплексного числа примет вид:
Комплексные числа обладают также геометрическим смыслом. Для плоскости с прямоугольной системой координат можно заметить, что какому-либо комплексному числу соответствует на ней точка с координатами x,y.
Радиус-вектор r комплексного числа является вектором, соединяющим начало координат с точкой на плоскости, соответствующей числу. Плоскость называют комплексной. В этом случае расположение действительных чисел совпадает с горизонтальной (или вещественной) осью. Мнимые части расположены по вертикали, то есть на мнимой оси.
Попробуем вычислить модуль числа:
z=3-25i
В этом случае:
- — действительная часть;
- — мнимая часть.
Тогда модуль определяется следующим образом:
.
Заметим, что в случае, когда действительное число равно z, модуль такого числа r=|z| является его абсолютной величиной. Например:
z=-7
r=|-7|=7.
Модуль обладает рядом полезных свойств, удобных для использования в процессе решения задач:
Разберем задание на умножение модулей пары комплексных чисел:
Выполним вычисления модулей для первого и второго числа:
В результате:
Используя понятия модуля и аргумента, выразим вещественные числа x, y комплексного числа z=x+iy:
Аргумент комплексного числа обладает следующими свойствами:
- .
- Точность определения аргумента комплексного числа составляет .
- Аргумент нельзя определить, если z=0.
- Ключевым значением аргумента является число . В том случае, когда речь идет об обратном числе, выполняется свойство: .
С комплексными числами, которые записаны в тригонометрической форме, можно выполнять разные действия. Рассмотрим те, которые наиболее часто встречаются в задачах.
Попробуем умножить два комплексных числа с помощью записанного правила:
Выполним вычисления:
Допустим, что число z является комплексным и записано в тригонометрической форме:
При этом его модуль равен:
С помощью формулы Эйлера получим:
Если число является комплексным, то справедливым будет следующее равенство:
Если z представляет собой вещественное число , то верно следующее соотношение:
В том случае, когда z является мнимым числом , применимо следующее соотношение:
С помощью формулы Эйлера запишем:
Попробуем на примере конкретного комплексного числа z=2i выполнить перевод в показательную форму. В данном случае:
действительная часть
мнимая часть
Определим модуль и аргумент данного числа:
В результате, показательная форма числа примет вид:
Дополнительные формулы сокращенного умножения
Есть три основные дополнительные ФСУ – это бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых, а также формула разности n-ых степеней двух слагаемых. Коротко о каждой из них.
Бином Ньютона
Бином Ньютона – это формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Выглядит она следующим образом:
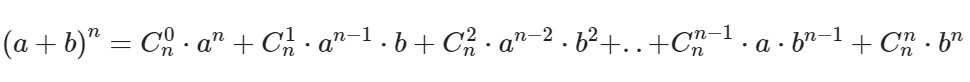
Ck в степени n – это биноминальные коэффициенты, стоящие в строке под номером n в треугольнике Паскаля. Вычисляются эти коэффициенты по формуле:
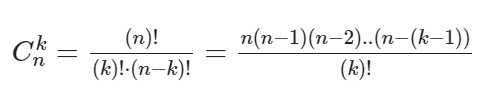
Иначе говоря, ФСУ для квадрата и куба разности и суммы являются частными случаями формулы бинома Ньютона при n=2 и n=3 соответственно.
Однако может быть так, что слагаемых в сумме, которую нужно возвести в степень, больше, чем два. В таком случае подойдет формула квадрата суммы трех, четырех и более слагаемых.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Как и было сказано, формула возведения в квадрат суммы трех, четырех и более слагаемых нужна, когда слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
Выглядит она так:
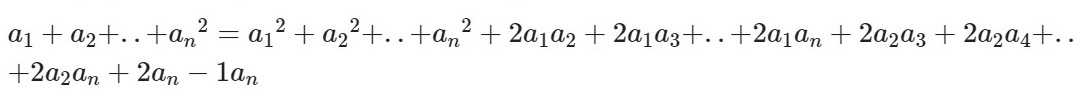
Читать и запоминать эту формулу нужно следующим образом: квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
И последняя формула – это формула разности n-ых степеней двух слагаемых, выглядящая вот так:
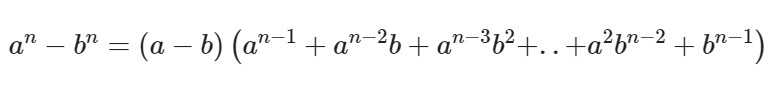
Как правило, данную формулу разделяют на две отдельные: для четных и нечетных степеней.
Формула для четных показателей 2m:
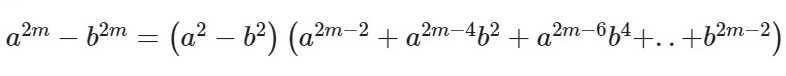
Формула для нечетных показателей 2m + 1:
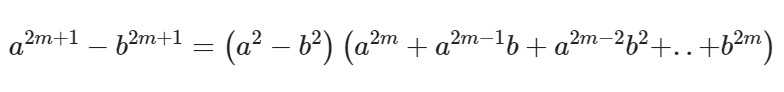
Несложно догадаться, что ФСУ разности квадратов и кубов являются частными случаями данной формулы при n=2 и n=3 соответственно. А для разности кубов b заменяется на –b.
Рассмотренные нами ФСУ и дополнительные ФСУ обязательно помогут вам быстрее справляться с математическими задачами и занимать свой мозг полезной деятельностью.
Умножение числа на само себя
Умножение числа на само себя называется возвести во вторую степень. Это одна из операций арифметики, которая позволяет получить результат, умножив число на само себя.
Чтобы возвести число во вторую степень, нужно число умножить само на себя: число во второй степени равно числу, умноженному само на себя. Например, если у нас есть число 5, то его вторая степень будет равна 5 * 5 = 25.
Возведение числа во вторую степень часто используется в математике и на практике. Например, чтобы найти площадь квадрата со стороной 5, нужно возвести эту сторону во вторую степень: 5 * 5 = 25. Также, возводя число во вторую степень, можно найти квадратный корень из этого числа.
Важно отметить, что возведение числа во вторую степень является одним из простых примеров. В математике существуют также более сложные операции, такие как возведение числа в третью степень, четвертую степень и т.д
Операция умножения является одной из основных арифметических операций. Она позволяет найти результат умножения двух чисел. В контексте темы «Как называют число во второй степени?», умножение числа на само себя называется возведением во вторую степень.
Например, если мы возведем число 2 во вторую степень, то получим результат равный 4. Это значит, что число 2, умноженное на само себя, равно 4. Этот процесс и результат называются возведением числа во вторую степень.
В математике возведение числа во вторую степень обычно обозначается с помощью символа «^». Так, число 2 во второй степени записывается как 2^2. Результат умножения числа 2 на само себя равен 4, поэтому 2^2 равно 4.
Операция умножения и возведение во вторую степень являются основными элементами математических вычислений. Они широко применяются в различных областях, таких как физика, экономика, информатика и другие. Использование возведения числа во вторую степень позволяет решать задачи и производить различные расчеты, где число встречается второй раз. Знание этой операции полезно и необходимо для развития математической грамотности и умений.
Примеры умножения чисел на себя
Умножение числа на себя называется возведением во вторую степень. Это математическая операция, которая позволяет получить результат умножения числа на само себя. Например, число 5 во второй степени обозначается как 5^2 и равно 25.
Также можно выразить число во второй степени с помощью операции умножения: 5 * 5 = 25. То есть, число 5 умножается на само себя и результатом является число 25.
Примеры умножения чисел на себя можно представить в виде таблицы:
| Число | Во второй степени |
|---|---|
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
Из примеров видно, что при возведении чисел во вторую степень результат всегда будет больше исходного числа. Например, 2 во второй степени равно 4, а 3 во второй степени равно 9. Это связано с тем, что при умножении числа на само себя результат будет всегда положительным.
Возведение чисел во вторую степень широко применяется в математике и науке, а также в программировании и инженерных расчетах. Это позволяет удобно работать с большими числами и получать точные результаты при выполнении сложных вычислений.
Побитовое исключающее «или»
В программировании и математике символ «^» означает побитовое исключающее «или». Он используется для выполнения операции побитового исключающего «или» между двумя числами.
Операция побитового исключающего «или» выполняется путем сравнения двоичных представлений чисел. Если биты в соответствующих позициях различны, то результат будет 1, в противном случае — 0.
Операция побитового исключающего «или» может быть использована для различных целей, таких как обмен значениями переменных без использования дополнительной переменной или реализация простой шифровальной функции.
Чтобы побитово исключающее «или» работало правильно, числа должны быть в двоичной форме. Операция выполняется для каждого бита числа, начиная с младшего бита (самого правого) и двигаясь к старшему биту (самому левому).
Что такое побитовое исключающее «или»?
Побитовое исключающее «или» — это операция, которая выполняется над двоичными числами. Она позволяет получить новое число, состоящее из битов, которые присутствуют только в одном из исходных чисел.
Для понимания этой операции, нужно знать, что двоичное число представляет собой последовательность единиц и нулей. Каждый бит (цифра в числе) представляет определенную степень числа 2. Например, число 1010 представляет собой сумму чисел 8, 0, 2 и 0.
Используя побитовое исключающее «или», можно выполнить операцию, аналогичную сложению или умножению чисел. Операция позволяет складывать биты, но без учета переноса или умножать биты, но без учета разрядности чисел.
Пример использования побитового исключающего «или»:
| Число A | Число B | Результат |
|---|---|---|
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
Таким образом, побитовое исключающее «или» выполняет операцию над каждым битом исходных чисел и возвращает новое число, в котором каждый бит принимает значение, отличное от бита второго числа.
Как использовать символ ^ в побитовых операциях?
Символ ^ в побитовых операциях используется для выполнения операции «исключающее ИЛИ» между двумя числами. Эта операция выполняется побитово, то есть каждый бит двух чисел сравнивается и на выходе получается новое число, в котором каждый бит равен 1, только если биты исходных чисел различаются.
Например, если у нас есть два числа: 5 (бинарное представление: 101) и 3 (бинарное представление: 011), операция «исключающее ИЛИ» с помощью символа ^ даст нам результат 6 (бинарное представление: 110). Это означает, что каждый бит в результате равен 1 только если биты в исходных числах отличаются.
Также символ ^ можно использовать для выполнения побитовой операции «побитовое ИСКЛЮЧАЮЩЕЕ ИЛИ» между числом и самим собой. В этом случае результат будет равен 0 для каждого бита числа. Например, если у нас есть число 9 (бинарное представление: 1001), то операция 9 ^ 9 даст результат 0 (бинарное представление: 0000).
Таким образом, символ ^ в побитовых операциях позволяет выполнять операцию «исключающее ИЛИ» или «побитовое ИСКЛЮЧАЮЩЕЕ ИЛИ» между двумя числами, а также выполнить операцию «побитового ИСКЛЮЧАЮЩЕГО ИЛИ» между числом и самим собой.
Использование операции возведения в степень
Операция возведения в степень является одной из основных математических операций. Она позволяет получать результат второй степени числа. Данная операция применяется в различных областях, таких как алгебра, физика, программирование и т.д.
В математике число, возводимое во вторую степень, называется основанием. При помощи операции возведения в степень число во второй степени можно найти путем умножения данного числа на себя. Например, число 2, возведенное во вторую степень, будет равно 4.
В программировании операцию возведения числа во вторую степень можно выполнить при помощи специальных функций или операторов. Например, в языке программирования Python оператор ** используется для возведения числа в степень. Также возведение числа во вторую степень можно выполнить с помощью функции pow(), передавая в нее число и степень в качестве аргументов.
Операция возведения в степень имеет свои особенности. Например, при возведении отрицательного числа во вторую степень результат будет положительным числом, так как отрицательное число возводится в квадрат и становится положительным. Также стоит отметить, что возведение числа в степень может быть выполнено для дробных чисел или чисел с плавающей точкой.
Использование операции возведения в степень позволяет проводить различные математические вычисления, решать задачи и упрощать сложные операции. Понимание принципа работы операции возведения в степень и умение применять ее в реальных задачах является необходимым навыком для успешного изучения математики, физики и программирования.
Операция возведения в степень
В математике операция возведения числа в степень позволяет увеличить число в разы, умножив его само на себя несколько раз. Например, число 2, возведенное в степень 2, равно 4. Такое число также можно назвать число, возведенное во вторую степень.
Операция возведения в степень обозначается символом ^. Например, 2^2 означает 2 в степени 2. В результате этой операции получается новое число, которое является произведением данного числа на само себя. Таким образом, 2^2 равно 2 * 2 = 4.
Степень может быть любым целым числом. Если степень положительная, то число возводится в эту степень. Если степень отрицательная, то число возводится в обратную степень, то есть полученное число вовзодится в отрицательную степень. Если степень равна нулю, то результат равен 1.
Операция возведения числа в степень позволяет упрощать и упорядочивать выражения и задачи в математике. Она имеет много практических применений и является основной для решения множества задач и проблем.
Примеры использования операции возведения в степень
В математике существуют различные операции с числами. Одной из таких операций является возведение числа в степень. Во второй степени это число умножается само на себя. Так, число 2 во второй степени будет равно 4.
Возведение в степень второй является часто используемой операцией в науке и технике. Например, в физике это позволяет вычислять площадь квадрата или площадь боковой поверхности куба.
Кроме того, возведение числа во вторую степень может иметь и другие применения. Например, в алгоритмах для определения расстояния между точками на плоскости используется формула, в которой необходимо возвести разность координат в квадрат.
Также возведение во вторую степень используется в задачах теории вероятностей. Например, для определения вероятности наступления определенного события можно возвести вероятность этого события в квадрат.
Использование операции возведения в степень во вторую позволяет получать новые значения чисел и применять их в различных областях знаний. Знание основ математики и операций с числами поможет лучше понимать и использовать эту операцию в практических задачах.






























