Функция
Разберем определение подробнее:
— Что значит «…зависимость переменной \(y\) от переменной \(x\)…»?
Наглядный пример: предположим, вы пришли в магазин купить конфеты, которые продаются вразвес и стоят по \(100\) рублей килограмм. Вопрос – сколько денег вы заплатите? Ответ: смотря сколько конфет купим! Действительно, купим два килограмма – заплатим \(200\) рублей, купим четыре с половиной – заплатим \(450\) рублей. То есть, цена покупки зависит от количества килограмм. Или, иначе говоря, цена покупки есть функция от количества купленных килограмм.
И если количество килограмм обозначить за \(x\), а цену покупки — за \(y\), то можно записать: \(y=100x\). Фактически, эта запись и есть функция. При этом понятно, что \(x\) изменяется по нашему желанию. Поэтому:
\(y\) называется зависимой переменной или функцией икса.


Эту связь между иксом и игреком можно пояснить такой аналогией: игрек – это телевизор, а икс – пульт от него. И если вы хотите, например, увеличить звук — вы не лезете внутрь телевизора и не пытаетесь вручную поменять напряжение в его резисторах, а просто нажимаете кнопку на пульте – и звук меняется. То есть звук поменялся не сам по себе, а потому что вы нажали кнопку. При этом с самим телевизором вы ничего не делали.
— Что значит «…каждому значению \(x\) соответствует только одно значение \(y\)»? Если мы в полученную выше функцию \(y=100x\) поставим вместо икса, например, тройку, то получим, что игрек равен \(100·3=300\). И сколько бы раз мы не подставляли вместо икса тройку – мы всегда будем получать, что игрек равен \(300\). Мы никак не сможем получить другое значение игрека, если будем подставлять один и тот же икс. В этом и заключается смысл записи «каждому значению икса – только одно значение игрека».
Отметим, что игрек может быть одинаков для нескольких иксов. Например, функция \(y=x^2-6x+9\) имеет одинаковые значения игрека для икса равного \(1\) и для икса равного \(5\).
Однако это никак не противоречит сказанному выше: сколько бы мы не подставляли вместо икса \(1\) или \(5\) – мы всегда будем получать только «игрек равен \(4\)».
Вообще понятие функции гораздо шире рассмотренного выше, потому что функцией можно назвать не только «вычисления по формуле», но и любую зависимость элементов. При этом обязательно должно выполняться требование «одному иксу – один игрек». Для ясности приведем еще несколько примеров из жизни.
Например, зависимость типа «человек» — «рост человека» вполне можно считать функцией, потому что для каждого «икса» (то есть каждого отдельного человека) есть свой «игрек» (рост этого человека). Причем значение игрека (роста) определяется тем, какой икс (то есть какого именно человека) мы взяли, и это значение — только одно.
А вот зависимость типа «человек» — «хобби человека» уже не функция! Потому что требование «одному иксу – один игрек» здесь не выполняется, ведь у человека (икса) может быть и два, и три, и десять разных хобби (игреков).
Еще пример: вы шли по улице и нашли \(100\) рублей. Значит ли это, что пройдя по этой улице \(10\) раз, вы найдете \(1000\) рублей? Нет, не значит, потому что здесь нет зависимости между прогулкой и найденной суммой. Это случайность, а не функция.
Еще один важный момент
Еще раз повторю определение и сделаю на нем акцент:
Заметил? Слово «единственный» – это очень-очень важный элемент нашего определения. Постараюсь объяснить тебе на пальцах.
Допустим, у нас есть функция, заданная прямой. \( \displaystyle y=5x+3\). При \( \displaystyle x=0\), мы подставляем данное значение в наше «правило» и получаем, что \( \displaystyle y=3\).
Одному значению \( \displaystyle x\) соответствует одно значение \( \displaystyle y\). Мы даже можем составить таблицу различных значений и построить график данной функции, чтобы убедится в этом.
| \( \displaystyle x\) | \( \displaystyle 0\) | \( \displaystyle 1\) | \( \displaystyle -1\) | \( \displaystyle 2\) | \( \displaystyle -2\) |
| \( \displaystyle y\) | \( \displaystyle 3\) | \( \displaystyle 8\) | \( \displaystyle -2\) | \( \displaystyle 13\) | \( \displaystyle -7\) |
А вот и график с нашими отмеченными точками:
Как ты убедился – графиком является прямая, в которой одному значению \( \displaystyle x\) соответствует одно значение \( \displaystyle y\) (данный факт показан красными линиями).
Соответственно, данная зависимость подходит под определение функции.
А что ты скажешь о такой зависимости: \( \displaystyle y=2{{x}^{2}}-4{x}-1\), то есть параболы? Является ли она функцией? Давай составим также табличку значений:
| \( \displaystyle x\) | \( \displaystyle 0\) | \( \displaystyle 1\) | \( \displaystyle -1\) | \( \displaystyle 2\) | \( \displaystyle -2\) |
| \( \displaystyle y\) | \( \displaystyle -1\) | \( \displaystyle -3\) | \( \displaystyle 5\) | \( \displaystyle -1\) | \( \displaystyle 15\) |
«Смотри! – скажешь ты, – « \( \displaystyle -\mathbf{1}\)» встречается два раза!» Так быть может парабола не является функцией? Нет, является!
То, что «\( \displaystyle -1\)» встречается два раза далеко не повод обвинять параболу в неоднозначности!
Дело в том, что, при расчёте для \( \displaystyle x=0\), мы получили один игрек. И при расчёте с \( \displaystyle x=2\) мы получили один игрек. Так что все верно, парабола является функцией.
Посмотри на график:
Разобрался? Если нет, вот тебе жизненный пример сооовсем далекий от математики!
Допустим, у нас есть группа абитуриентов, познакомившихся при подаче документов, каждый из которых в разговоре рассказал, где он живет:
Согласись, вполне реально, что несколько ребят живут в одном городе, но невозможно, чтобы один человек жил в нескольких городах одновременно. Это как бы логичное представление нашей «параболы» – нескольким разным икс соответствует один и тот же игрек.
Теперь придумаем пример, когда зависимость не будет функцией. Допустим, эти же ребята рассказывали, на какие специальности они подали документы:
Здесь у нас совершенно другая ситуация: один человек может спокойно подать документы как на одно, так и на несколько направлений. То есть одному элементу \( \displaystyle x\) множества \( \displaystyle X\) ставится в соответствие несколько элементов \( \displaystyle y\) множества \( \displaystyle Y\). Соответственно, это не функция.
Проверим твои знания на практике. Определи по рисункам, что является функцией, а что нет:
Разобрался? А вот и ответы:
- Функцией является – В, Е.
- Функцией не является – А, Б, Г, Д.
Почему? Да вот почему:
На всех рисунках кроме В) и Е) на один \( \displaystyle x\) приходится несколько \( \displaystyle y\)!
Уверена, теперь ты с легкостью отличишь функцию от «НЕ функции», скажешь, что такое аргумент и что такое зависимая переменная, а так же определишь область допустимых значений аргумента и область определения функции.
Замена переменных в тройном интеграле и цилиндрические координаты
Если проекцией области интегрирования на какую-либо из координатных плоскостей
является круг или часть круга, то тройной интеграл проще вычислисть, перейдя к цилиндрическим координатам.
Цилиндрическая система координат является обобщением полярной системы координат
на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами
(r, φ, z), где r — расстояние от начала координат до проекции N
точки M на плоскость xOy, φ — угол между вектором ON и положительным
направлением оси Ox, z — аппликата точки M (рисунок ниже).
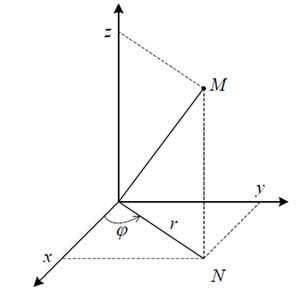
Прямоугольные координаты x, y, z с цилиндрическими
координатами r, φ, z связывают формулы
,
,
.
Для того, чтобы в тройном интеграле перейти к цилиндрическим координатам, нужно
подынтегральную функцию выразить в виде функции переменных r, φ, z:
.
То есть переход от прямогольных координат к цилиндрическим осуществляется следующим образом:
.
Тройной интеграл в цилиндрических координатах вычисляется так же как и в декартовых
прямоугольных координатах, путём преобразования в последовательность трёх определённых интегралов:
Пример 8. Вычислить тройной интеграл
переходом к цилиндрическим координатам, где —
область, ограниченная поверхностями и
.
Решение. Так как область на плоскость xOy
проектируется в круг , то
координата φ изменяется в пределах от 0 до 2π, а координата r — от r=0 до
r=1. Постоянному значению
в пространстве соответствует цилиндр .
Рассматривая пересечение этого цилиндра с областью , получаем изменение
ординаты z от до
. Переходим к цилиндрическим координатам и получаем:
Ответ: данный тройной интеграл равен π/6.
Как найти производную функции, заданной неявно
Будем учиться находить производные функций, заданных неявно. Что значит неявно?
Сравним с обычной функцией. Обычная функция задана уравнением вида ,
где игрек, то есть функция, задан некоторым выражением, в котором присутствует икс. Таким образом,
из переменных в левой части — только игрек, в правой — только икс. Если же функция задана неявно, то в
левой части различные слагаемые с игреком «смешаны» с различными слагаемыми с иксом (или переменной,
обозначенной другой буквой). Примеры функций, заданных неявно:
,
,
,
,
.

При этом и икс, и игрек могут быть в различных степенях, а в одном слагаемом могут быть
и игрек, и икс.
Если функция задана неявно, то как получить игрек, то есть явную функцию? Просто:
выразить игрек через другую переменную, то есть получить в левой части только игрек. А если нужно найти
производную функции, заданной неявно, то есть получить в левой части только игрек со штрихом? Нужно сначала
найти производные обеих частей уравнения, то есть продифференцировать их. А затем выразить производную
игрека через производные других переменных.
Теперь приведенный выше «скелет» решения обрастет «мясом», то есть необходимыми
подробностями. Те слагаемые, в
которых присутствует только икс, обратятся в обычную производную функции от икса. А слагаемые, в которых
присутствуют и икс, и игрек, нужно дифференцировать, пользуясь правилом дифференцирования сложной функции,
то есть учитывать, что игрек — это функция от икса. Если совсем просто, то в полученной производной
слагаемого с иксом должно получиться: производная функции от игрека, умноженная на производную от игрека. Например, производная слагаемого
запишется как
, производная
слагаемого запишется как
. Далее из всего этого
нужно выразить этот «игрек штрих» и будет получена искомая производная функции, заданной неявно.
Разберём это на примерах.
Использование икса в науке
Икс является одним из основных символов, используемых в науке. Он обозначает неизвестное значение или переменную в математических уравнениях и формулах. Также икс может быть использован для обозначения неизвестного фактора или переменной в других научных дисциплинах, таких как физика, химия или биология.
В математике икс используется для обозначения переменных, которые могут принимать различные значения. Использование икса позволяет создавать алгебраические уравнения и решать их с помощью методов алгебры и анализа. Например, в уравнении x + 2 = 5, икс обозначает неизвестное значение, которое мы должны определить, чтобы уравнение стало истинным. Решая это уравнение, мы находим, что x = 3.
В физике икс может обозначать неизвестное значение или неизвестную переменную в уравнениях движения, законах сохранения или других законах физики. Например, в уравнении для свободного падения s = ut + (1/2)gt^2, икс обозначает неизвестное значение расстояния, u — начальную скорость, g — ускорение свободного падения, t — время. Решая это уравнение, мы можем определить значение икса и, следовательно, расстояния.
В химии икс может обозначать неизвестную переменную в уравнениях реакций или концентрации веществ. Использование икса в химических уравнениях позволяет определить неизвестное количество вещества или концентрацию, и таким образом, провести расчеты и провести анализ реакций.
Икс также может быть использован в других научных дисциплинах, чтобы обозначить неизвестные переменные или факторы, которые требуется определить через эксперименты или исследования.
Выводы:
- Икс широко используется в математике, физике, химии и других научных дисциплинах.
- Использование икса позволяет обозначать неизвестные значения или переменные в уравнениях и формулах.
- Решение уравнений с помощью икса позволяет определить значения неизвестных переменных в различных научных дисциплинах.
Кто придумал икс и игрек
02.05.2017 17:17 726
Кто придумал икс и игрек.
Если вы уже учитесь в школе, то вам наверняка знакомы две латинские буквы — «х» (Икс) и «у» (Игрек, так еще зовут одного из персонажей любимого многими ребятами мультика «Фиксики), которыми в задачках по математике обозначаются неизвестные числа. А знаете ли вы откуда они взялись?
Сама по себе идея обозначить неизвестное число буквой была известна ещё в античном мире.А впервые это сделал в III веке нашей эры александрийский математик Диофант.
Особым обозначением и названием наделяли неизвестные числа и такие народы, как древние египтяне, вавилоняне, индийцы, и жители Средней Азии.
Хотя если говорить честно, то в те времена древние греки вообще не знали цифр как таковых – т.е. у них не было отдельных знаков для обозначения чисел. Для этой цели они использовали…буквы, помещая над ними черту.
Буква «альфа» с чертой обозначала — 1, «бета» – 2 и т.д., с «иоты» начинались десятки, с буквы «ро» – сотни, и замыкала эту цепочку чисел буква сампи, соответствующая числу 900, она была 27-й по счету буквой греческого алфавита.
Однако, была ещё и 28-я буква – «сигма» концевая, которой числа не досталось… Вот её-то и стал использовать древний ученый Диофант для обозначения неизвестных чисел.
Точно так же, но уже в более поздние времена, обстояло дело и на Руси.То есть,вместо цифр использовали буквы. И так продолжалось, пока править не начал Петр Великий. Буквенные обозначения неизвестных чисел применялись и математиками Европы XV–XVI (15-16) веков.
Привычная же нам система математических символов связана с французским математиком XVII (17) века Рене Декартом. После того, как в своих трудах он окончательно установил буквы х (икс) и у (игрек) в качестве знаков обозначения неизвестых чисел, они были приняты в средневековой Европе.
Историки предполагают, что обозначение неизвестного числа буквой «икс» связано с традициями арабской математики.
Дело в том, что арабы обозначали все неизвестное словом «нечто», по-арабски – «шей», а для письменного обозначения использовали букву, произносившуюся как «ш».
Через Испанию, над которой долгое время властвовала арабская Мавритания, эти достижения усвоили европейцы. Однако, для обозначения арабского «шэй» испанцы использовали латинскую букву «x», которая в то время читалась у них как «ш».
Вполне возможно, что под влиянием именно этой традиции Декарт стал обозначать неизвестные числа буквами «х» — икс и «у» — игрек.

Икс или игрек
Смотреть что такое «Икс или игрек» в других словарях:
Икс — Иксъ (иноск.) неизвѣстный (намекъ на алгебр. знакъ и формулы). Ср. Каждый день вынимаю я изъ шкатулки. мое выкупное свидѣтельство (и думаю), мнѣ ли оно принадлежитъ, или какому то иксу, котораго я даже назвать по имени не могу. Салтыковъ.… … Большой толково-фразеологический словарь Михельсона (оригинальная орфография)
ИГРЕК — ИПСИЛОН или ИГРЕК (?, у) 25 я буква немецкого и 24 я латинского алфавитов. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. игрек (фр. i grec греческое и ) предпоследняя буква латинского алфавита (у); в математике… … Словарь иностранных слов русского языка
игрек — икс I. (иноск.) неизвестный (намек на алгебр. знак и формулы) Ср. Каждый день вынимаю я из шкатулки. мое выкупное свидетельство (и думаю), мне ли оно принадлежит или какому то иксу, которого я даже назвать по имени не могу. Салтыков. Сборник.… … Большой толково-фразеологический словарь Михельсона
ИКС — Латинская буква, которой обозначается в математике неизвестная или искомая величина. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ИКС буква латинского алфавита, употребляемая обыкновенно в математике для… … Словарь иностранных слов русского языка
икс — а, м. X. 1. Название третьей с конца буквы латинского и французского алфавита. В сравн. Всмотритесь пристально в этот табурет вида Х, и признайтесь что до нынешняго столетия никогда еще не было дойдено до того чтобы сидеть в одно время между… … Исторический словарь галлицизмов русского языка
икс — I. (иноск.) неизвестный (намек на алгебр. знак и формулы) Ср. Каждый день вынимаю я из шкатулки. мое выкупное свидетельство (и думаю), мне ли оно принадлежит или какому то иксу, которого я даже назвать по имени не могу. Салтыков. Сборник. Дети… … Большой толково-фразеологический словарь Михельсона
игрек — а, м. 1) Название предпоследней буквы латинского алфавита: y, y. 2) мат. Символ для обозначения неизвестной или переменной величины (наряду с x, z). Уравнение с игреком. 3) В литературном произведении: условное обозначение неизвестного или… … Популярный словарь русского языка
икс — а, мн. и/ксы, ов, м. 1) Название третьей от конца буквы латинского алфавита: X, x 2) мат. Символ для обозначения неизвестной или переменной величины (наряду с y, z). Уравнение с иксом. 3) В литературном произведении: условное обозначение… … Популярный словарь русского языка
Выразить переменную из уравнения
При решении систем линейных уравнений с многими переменными возникает частая необходимость выражения из уравнения той или иной переменной.
Как это делается? Возьмем для примера уравнение 2x+10y+3z=10. В нем наличествуют три переменных X, Y, Z. При помощи онлайнового калькулятора в зависимости от потребности выражения той или иной переменной уравнение 2x+10y+3z=10 преобразуется: — через z в уравнение вида z = (-2x-10y+10)/(+3); — через y в уравнение вида y = (-2x-3z+10)/(+10); — через x в уравнение вида x= (-10y-3z+10)/(+2).
Полученное значение переменной X, Y или Z можно подставлять в следующее уравнение системы. В результате в нем будет на одну неизвестную переменную меньше. Выражение переменной из уравнений требуется при решении задач линейного программирования, направленных на выяснение значений показателей эффективности (целевой функции) в самых различных направлениях.
Решение систем линейных уравнений требуется для целей определения важных показателей сложных практических производственных и иных задач: — загрузки оборудования, — планирования производств, — составления пищевого рациона откармливаемых животных, — использования сырья и пр.
Примеры использования икс и игрек в реальной жизни
Математические переменные икс (x) и игрек (y) являются базовыми понятиями в алгебре и используются для обозначения неизвестных или произвольных значений в уравнениях и графиках. Они имеют широкое применение в различных областях науки и повседневной жизни. Вот несколько примеров использования икс и игрек в реальной жизни:
- Анализ данных: При анализе данных и построении статистических моделей, икс и игрек часто используются для представления независимых и зависимых переменных соответственно. Например, в экономической науке икс может обозначать количество произведенных товаров, а игрек — цену этих товаров. Используя икс и игрек, можно определить зависимость между количеством произведенного товара и его ценой.
- Графика и моделирование: В графике икс и игрек обычно используются для обозначения координат точек на плоскости. Икс обозначает горизонтальную ось, а игрек — вертикальную ось. Например, при построении графика функции y = f(x), икс будет обозначать значения аргумента функции, а игрек — соответствующие значения функции. Это позволяет визуализировать и анализировать зависимость между переменными.
- Инженерные расчеты: В инженерии икс и игрек широко применяются при решении уравнений и моделировании физических процессов. Например, при расчете траектории полета ракеты, икс может обозначать время, а игрек — высоту полета. Моделирование таких процессов позволяет инженерам проводить анализ и оптимизацию систем и изделий.
- Финансовые расчеты: В финансовых расчетах икс и игрек используются для моделирования и прогнозирования финансовых показателей. Например, при анализе финансовых потоков икс может обозначать время, а игрек — денежный поток. Используя икс и игрек, можно определить прибыльность и эффективность инвестиций.
Как видно из этих примеров, икс и игрек играют важную роль в анализе данных, моделировании и прогнозировании различных процессов. Они помогают упростить и структурировать сложные математические концепции, позволяя исследователям и специалистам анализировать и объяснять различные явления и взаимосвязи в реальном мире.
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)
Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.
Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики. На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях). Мы рассмотрим:
- степенную функцию (линейную, квадратичную, обратную зависимость, корни),
- тригонометрические и обратные тригонометрические,
- показательную и
- логарифмическую функции.
Преобразования графиков функций (ЕГЭ 18. Задачи с параметром)
Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль?
Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?
Можно! И на этом уроке мы научимся производить такие трансформации.
Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.
Практические рекомендации
Если вы сталкиваетесь с уравнением, где равенство между игреком и икс не выполняется, то ваша задача — найти такие значения, которые сделают уравнение истинным. Это может быть сложно, но переставление переменных и применение правил алгебры могут помочь.
Если вы видите график уравнения, то равенство игрека и икс говорит о том, что точка на графике находится на линии y=x, которая пересекает этот график. Если вы находитесь на этой линии, то значит для каждого значения икса, значение игрека будет такое же, что означает, что график симметричен относительно этой линии.
При решении задач на равенство игрека и икс важно быть внимательным и не допустить ошибок. Например, в некоторых случаях, ожидаемое решение может оказаться противоположным к тому, что вы предполагали в начале
Поэтому, проверка своих ответов — это еще одна важная рекомендация.
- Проверьте, выполняется ли равенство игрека и икс в вашем уравнении.
- Если оно не выполняется, используйте алгебру, чтобы найти значения, которые сделают равенство истинным.
- Наблюдайте за графиком уравнения для лучшего понимания равенства игрека и икс.
- Не забывайте проверять свои ответы и не допускать ошибки!
И наконец, практика — это самое лучшее средство для научиться решать задачи на равенство игрека и икс. Попробуйте решить несколько примеров, чтобы понять, как это работает на практике. Удачи вам в изучении математики!
Нахождение вершины параболы: способы, примеры, советы
График функции y = ax 2 + bx + c, где a — первый коэффициент, b — второй коэффициент, c — свободный член, называется параболой
Но обратите внимание на тот факт, что a ≠0
У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.
Первый способ
Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.
Например, y =x 2 –8 x +15;
находим первый, второй коэффициенты и свободный член;
подставляем значения a и b в формулу;
вычисляем значения y;
Значит, вершина находится в точке (4;-1).
Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n — корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.
Рассмотрим на примере y =x 2 –6x+5
1) Приравниваем к нулю:
2) Находим дискриминант, используя формулу: D = b 2 –4 ac:
3) Находим корни уравнения по формуле (-b±√ D)/2a:
- 1 — первый корень;
- 5 — второй корень.
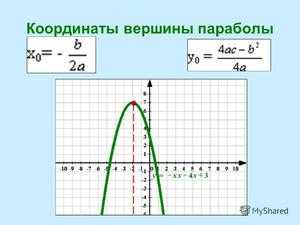
Второй способ
Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.
1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x 2 + 8x = -10.
2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.
У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:
3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.
4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).
Третий способ
Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:
1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.
2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.
Рассмотрим этот способ подробнее.
Дана функция y = 4x²+16x-17;
Записываем производную и приравниваем к нулю.
f'(x) = (4x²+16x-17)’ = 8x+16 =0

Икс в компьютерных науках и программировании
В компьютерных науках и программировании символ «икс» (X) часто используется для обозначения различных значений и переменных. Он служит для обозначения неизвестных или изменяемых значений в алгоритмах и программном коде.
Переменные и икс
В программировании переменные играют важную роль. Они используются для хранения данных и изменения значений в процессе выполнения программы. Переменные могут быть именованными, например: «x», «y», «width», «height». Обычно символ «икс» используется для обозначения неизвестных значений или значений, которые будут определены в ходе выполнения программы.
Пример использования переменной «x» в программировании:
int x = 10; // объявление переменной «x» и присвоение ей значения 10
x = x + 5; // изменение значения переменной «x» на 15
В этом примере переменная «x» инициализируется значением 10, а затем её значение изменяется на 15
Обратите внимание на использование символа «икс» для обозначения переменной
Икс в алгоритмах
В алгоритмах символ «икс» также может использоваться для обозначения неизвестных значений или неизвестных параметров. Например, в алгоритмах поиска или сортировки, значение «икс» может представлять неизвестный элемент или значение, которое нужно найти или определить.
Пример использования символа «икс» в алгоритме поиска:
function linearSearch(arr, x) {
for (let i = 0; i
if (arr === x) {
return i; // возвращаем индекс элемента, если найден
}
}
return -1; // возвращаем -1, если элемент не найден
}
В этом примере символ «икс» используется для обозначения искомого значения в алгоритме линейного поиска.
Икс в математических выражениях
Символ «икс» также широко используется в математических выражениях и формулах в программировании. Он обозначает переменную или неизвестное значение, которое может меняться в зависимости от контекста.
Пример использования символа «икс» в математическом выражении:
function quadraticEquation(a, b, c) {
let x1 = (-b + Math.sqrt(b*b — 4*a*c)) / (2*a);
let x2 = (-b — Math.sqrt(b*b — 4*a*c)) / (2*a);
return ; // возвращаем корни квадратного уравнения
}
В этом примере символ «икс» используется для обозначения корней квадратного уравнения. Значение «икс» будет определено в процессе выполнения программы в зависимости от входных параметров.





























